Túlzás, ami van. A fogalom jelentése

2024 Szerző: Henry Conors | [email protected]. Utoljára módosítva: 2024-02-12 08:30

A cikk a statisztika tudomány szerepét írja le. A kurtosis fogalmát és a tudományban való felhasználását megvizsgáljuk.

Statisztika. Alapkoncepció

A statisztika a matematikai tudomány alapvető származéka. Ez a tantárgy számos olyan társadalmi tudományághoz tartozik, amelyek célja a tanulók világképének kialakítása és az események kompetens elemzése.

A statisztika mindenféle folyamatot és eseményt tanulmányoz az emberek életében, kiemeli azok mintáit, és mindent bemutat rövid statisztikai jelentések formájában. Az ilyen tudomány társadalmilag hasznos és folyamatos fejlesztést igényel. Felesleg – mi ez? Ez egy alapfogalom a grafikus statisztikákban, amely segít meghatározni a tökéletes számítás helyességét. A kurtózisnak nem szabad erős eltérést mutatnia.

A statisztika lehetővé teszi, hogy kielégítse az emberek megbízható információk iránti igényét egy adott jelenségről, eseményről stb. Az élettényezők dinamikájának meghatározása, hanyatlásuk, stagnálásuk vagy növekedésük – pontosan ezt teszi ez a tudomány.

A modern világban a statisztika az egyik fő helyet foglalja el a tudományos színtéren. Tekintsük a „kurtosis” fogalmát. Mi a statisztikai cél és megfigyelés? Hol alkalmazzák ezeket a fogalmakat? Minderről bővebben itt olvashatcikk.

Mi a kurtosis a statisztikákban?

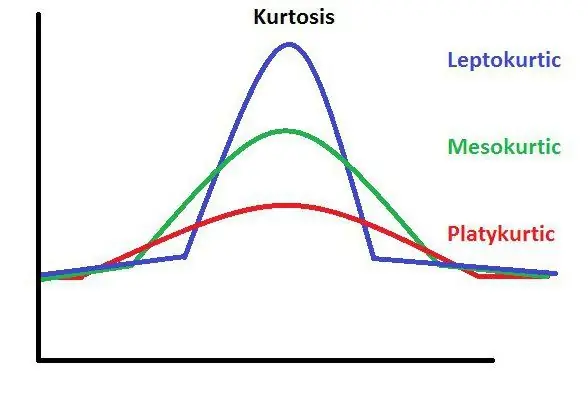
A kurtózis egy statisztikai fogalom, amely az eloszlási grafikon egyes csúcsainak élességét reprezentálja. Van egy speciális képlet a pontos kiszámításához.

Az elvárás azt állítja, hogy a statisztikai adatok egyenletesebb eloszlásához a kurtózisnak egyenlőnek kell lennie egy pozitív számmal. Szó szerint ez a fogalom a normától való bizonyos eltérést és a statisztikai rendszer további abnormális fejlődését vagy működését jelenti.

A statisztikai grafikonon túlzott kurtosis kifejezés hibás vizsgálatot vagy a grafikon eredeti adataiban szereplő hibákat jelezhet. Egy ilyen koncepció skaláris jellegű, ami azt jelenti, hogy a végső számításnak olyan számot kell eredményeznie, amely nem tartalmaz változókat vagy segédfüggvényeket. Így néz ki a kurtosis.

Mi a szimmetrikus és aszimmetrikus eloszlás

A kurtózis, amely a szimmetrikus típus eloszlásával kapcsolatos, egyenlő nullával. Ez egy grafikonon jól láthatóan megmutatható. Az aszimmetrikus grafikon olyan számot mutat, amely nem nulla. Így jelöljük a kurtosist.

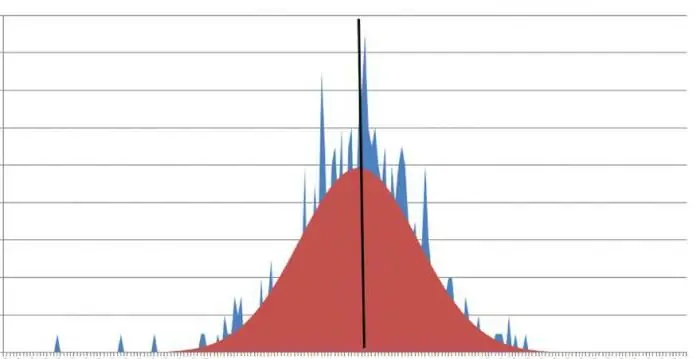
Mi a csúcs élessége? Az éles csúcsokkal rendelkező grafikon azt jelzi, hogy a kurtózis értéke nullánál kisebb szám. Gyakran vannak olyan helyzetek, amikor egy adott fogalom nem fejezhető ki külön értékkel. Ebben az esetben a mínusz vagy plusz végtelenhez közelít.